BAB 11 Statistical Training
BAB 11.
1.1. Filsafat mendasar
Ide dasar di balik pelatihan statistik (stochastic) dari jaringan saraf adalah: Perubahan bobot dan menjaga perubahan-perubahan yang meningkatkan kinerja. Kelemahan dari pendekatan ini adalahsangat lambat! Juga, itu bisa terjebak di minimum lokal jika perubahan acak kecil karena perubahan tidak mungkin memiliki daya yang cukup untuk mendaki "puncak" (lihat Gambar.)
untuk mencari nilai lain lembah. Untuk mengatasi terjebak dalam minimum lokal, perubahan berat badan yang besar dapat digunakan. Namun, kemudian jaringan dapat menjadi berosilasi dan kehilangan ketetapan minimal . Untuk menghindari ketidakstabilan ini mungkin, perubahan berat badan bisa turun secara bertahap dalam ukuran. Strategi ini menyerupai proses anil dalam metalurgi. Hal ini pada dasarnya berlaku untuk semua jaringan yang dijelaskan sebelumnya, tetapi khususnya hanya untuk propagasi dan dimodifikasi jaringan.
1.2. Metode anil
Dalam metalurgi, anil berfungsi untuk mendapatkan pencampuran yang diinginkan molekul untuk membentuk paduan logam. Oleh karena itu, logam pada awalnya diangkat ke suhu di atas nya, titik lebur. Dalam keadaan cair molekul terguncang , sehingga dalam jarak tinggi . Secara bertahap suhu berkurang dan akibatnya amplitudo gerak berkurang sampai logam mengendap di tingkat energi terendah. Gerak molekul diatur oleh distribusi probabilitas Boltzman.
p (e) = exp (-e / KT)
Dimana p (e) adalah probabilitas sistem berada di tingkat energi e. K menjadi Boltzman konstan, T yang menunjukkan temperatur absolut dalam derajat Kelvin (selalu positif). Dalam hal ini, jika T tinggi, exp (-e / KT) mendekati nol, sehingga hampir semua nilai e kemungkinan, yaitu adalah p (e) yang tinggi untuk setiap relatif tinggi e. Namun, ketika T berkurang, kemungkinan nilai tinggi e berkurang sejak e / KT meningkat sehingga exp (-e / KT) dikurangi untuk tinggi e.
11.3. Simulasi Annealing oleh Boltzman Pelatihan Berat
Kami menggantikan e Persamaan. dengan ΔE yang menunjukkan perubahan energi
fungsi E
p (ΔE) = exp (-ΔE / KT)
sementara T menunjukkan beberapa setara suhu. Sebuah latihan beban jaringan saraf
Prosedur demikian akan menjadi:
(1) Atur suhu setara T di beberapa nilai awal yang tinggi.
(2) Terapkan set input pelatihan untuk jaringan dan menghitung jaringan output, dan menghitung fungsi energi.
(3) Menerapkan perubahan berat badan secara acak Δw dan menghitung ulang sesuai keluaran dan fungsi energi (misalnya fungsi error kuadrat E = Σi (error) 2).
(4) Jika energi dari jaringan berkurang (untuk menunjukkan peningkatan kinerja)
kemudian terus Δw, lain: menghitung probabilitas p (ΔE) menerima Δw, melalui di atas dan pilih beberapa prosedur nomor acak r dari seragam distribusi antara 0 dan 1. Sekarang, jika p (ΔE)> r (catatan: ΔE> 0 dalam kasus peningkatan E) maka masih menerima perubahan di atas, yang lain, kembali ke sebelumnya nilai w.
(5) Pergi ke Langkah (3) dan ulangi untuk semua bobot dari jaringan, sementara secara bertahap mengurangiT setelah setiap set lengkap bobot telah (kembali) disesuaikan. Prosedur di atas memungkinkan sistem untuk sesekali menerima perubahan berat badan di arah yang salah (memburuknya kinerja) untuk membantu menghindari dari mendapatkan terjebak di minimum lokal. Pengurangan bertahap dari temperatur setara T mungkin deterministik (Setelah tingkat yang telah ditentukan sebagai fungsi dari jumlah iterasi).
11.4. Penentuan stokastik Besaran Berat Perubahan
Penyesuaian stokastik Δw (langkah 3 di di atas) juga dapat mengikuti termodinamika setara, di mana Δw dapat dianggap untuk mematuhi distribusi Gaussian:
p (Δw) yang menunjukkan kemungkinan perubahan berat badan Δw. Atau p (Δw) mungkin
mematuhi distribusi Boltzman serupa dengan ΔE. Dalam kasus ini, Langkah 3 adalah
dimodifikasi untuk memilih langkah perubahan Δw sebagai berikut [Metropolis et al., 1953].
- Pra-menghitung 1P distribusi kumulatif (w), melalui integrasi numerik
-Pilih nomor acak μ dari distribusi seragam pada interval dari 0 1. Gunakan nilai ini dari μ sehingga P (w) akan memuaskan, untuk beberapa w:
μ = P (w) (11,5)
dan mencari yang sesuai w ke P (w). Menunjukkan resultan w sebagai wk hadir untuk cabang saraf yang diberikan. Oleh karena itu, berasal
Δwk = wk - wk-1
wk-1 menjadi nilai bobot sebelumnya di cabang dipertimbangkan dalam jaringan.
11.5. Pengaturan suhu-Equivalent
Kami telah menyatakan bahwa pengurangan suhu bertahap merupakan dasar untuk Proses anil simulasi. Telah terbukti [Geman dan Geman 1984] yang untuk konvergensi ke minimum global, laju penurunan suhu-setara
harus memenuhi
k yang menunjukkan iterasi langkah.
1,6. Cauchy Pelatihan Neural Network
Karena pelatihan Boltzman dari jaringan saraf seperti pada Secs. 11,2-11,4 sangat lambat, metode stokastik cepat berdasarkan distribusi probabilitas Cauchy adalah diusulkan oleh Szu (1986). Distribusi Cauchy perubahan energi :
untuk menghasilkan fungsi distribusi lagi (surut lebih lambat) ekor daripada di kasus Boltzman atau distribusi Gaussian. Perhatikan bahwa untuk Cauchy distribusi:
var (ΔE) = ∞ !!
Ketika distribusi Cauchy digunakan untuk Δw, resultan Δw akan memuaskan
Δw = ρT · tan [p (Δw)] (11.9)
ρ menjadi koefisien tingkat belajar. Langkah (3) dan langkah (4) dari prosedur framing
dari Sec. 11.3 demikian akan menjadi:
(3.a) Pilih nomor n acak dari distribusi seragam antara 0 dan 1
dan biarkan
p (Δw) = n
dimana p (Δw) adalah dalam bentuk persamaan. (11.8) di atas
(3.b) Selanjutnya, menentukan Δw melalui Persamaan.) untuk memenuhi
Δw = ρT · tan (n) (11.11)
di mana T diperbarui oleh: T =Untuk1 + k ,untuk k = 1, 2, 3,. . . kontras dengan terbalik
tingkat Sec log. 11.5. Perhatikan bahwa algoritma baru untuk T mengingatkan kondisi Dvoretzky untuk
konvergensi dalam pendekatan stokastik [Graupe, 1989].
(4) Mempekerjakan Cauchy atau distribusi Boltzman di (4) dari Sec. 11.3. Metode pelatihan di atas adalah lebih cepat dari pelatihan Boltzman. Namun, masih sangat lambat. Selain itu, dapat mengakibatkan langkah ke arah yang salah menyebabkan ketidakstabilan. Karena Cauchy-mesin dapat menghasilkan Δw sangat besar, jaringan bisa mendapatkan terjebak. Untuk menghindari hal ini, batasan keras dapat ditetapkan. Atau, Δw dapat tergencet
M menjadi batas keras pada amplitudo Δw.




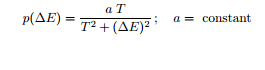



Komentar
Posting Komentar